program to draw binary search tree of a string
Construct Binary Tree from String with bracket representation
Construct a binary tree from a string consisting of parenthesis and integers. The whole input represents a binary tree. It contains an integer followed by zero, one or two pairs of parenthesis. The integer represents the root's value and a pair of parenthesis contains a child binary tree with the same structure. Always start to construct the left child node of the parent first if it exists.
Examples:
Input : "1(2)(3)" Output : 1 2 3 Explanation : 1 / \ 2 3 Explanation: first pair of parenthesis contains left subtree and second one contains the right subtree. Preorder of above tree is "1 2 3". Input : "4(2(3)(1))(6(5))" Output : 4 2 3 1 6 5 Explanation : 4 / \ 2 6 / \ / 3 1 5
We know first character in string is root. Substring inside the first adjacent pair of parenthesis is for left subtree and substring inside second pair of parenthesis is for right subtree as in the below diagram.
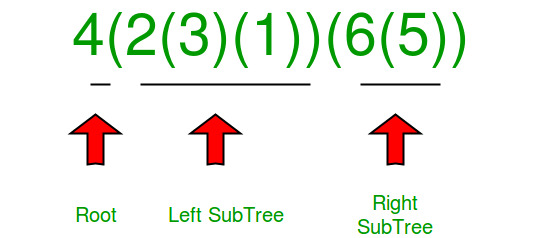
We need to find the substring corresponding to left subtree and substring corresponding to right subtree and then recursively call on both of the substrings.
For this first find the index of starting index and end index of each substring.
To find the index of closing parenthesis of left subtree substring, use a stack. Let the found index be stored in index variable.
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
Node *left, *right;
};
Node* newNode( int data)
{
Node* node = (Node*) malloc ( sizeof (Node));
node->data = data;
node->left = node->right = NULL;
return (node);
}
void preOrder(Node* node)
{
if (node == NULL)
return ;
printf ( "%d " , node->data);
preOrder(node->left);
preOrder(node->right);
}
int findIndex(string str, int si, int ei)
{
if (si > ei)
return -1;
stack< char > s;
for ( int i = si; i <= ei; i++) {
if (str[i] == '(' )
s.push(str[i]);
else if (str[i] == ')' ) {
if (s.top() == '(' ) {
s.pop();
if (s.empty())
return i;
}
}
}
return -1;
}
Node* treeFromString(string str, int si, int ei)
{
if (si > ei)
return NULL;
int num = 0;
while (si <= ei && str[si] >= '0' && str[si] <= '9' )
{
num *= 10;
num += (str[si] - '0' );
si++;
}
Node* root = newNode(num);
int index = -1;
if (si <= ei && str[si] == '(' )
index = findIndex(str, si, ei);
if (index != -1) {
root->left = treeFromString(str, si + 1, index - 1);
root->right
= treeFromString(str, index + 2, ei - 1);
}
return root;
}
int main()
{
string str = "4(2(3)(1))(6(5))" ;
Node* root = treeFromString(str, 0, str.length() - 1);
preOrder(root);
}
Java
import java.util.*;
class GFG
{
static class Node
{
int data;
Node left, right;
};
static Node newNode( int data)
{
Node node = new Node();
node.data = data;
node.left = node.right = null ;
return (node);
}
static void preOrder(Node node)
{
if (node == null )
return ;
System.out.printf( "%d " , node.data);
preOrder(node.left);
preOrder(node.right);
}
static int findIndex(String str, int si, int ei)
{
if (si > ei)
return - 1 ;
Stack<Character> s = new Stack<>();
for ( int i = si; i <= ei; i++)
{
if (str.charAt(i) == '(' )
s.add(str.charAt(i));
else if (str.charAt(i) == ')' )
{
if (s.peek() == '(' )
{
s.pop();
if (s.isEmpty())
return i;
}
}
}
return - 1 ;
}
static Node treeFromString(String str, int si, int ei)
{
if (si > ei)
return null ;
int num = 0 ;
while (si <= ei && str.charAt(si) >= '0' && str.charAt(si) <= '9' )
{
num *= 10 ;
num += (str.charAt(si) - '0' );
si++;
}
si--;
Node root = newNode(num);
int index = - 1 ;
if (si + 1 <= ei && str.charAt(si+ 1 ) == '(' )
index = findIndex(str, si + 1 , ei);
if (index != - 1 )
{
root.left = treeFromString(str, si + 2 , index - 1 );
root.right
= treeFromString(str, index + 2 , ei - 1 );
}
return root;
}
public static void main(String[] args)
{
String str = "4(2(3)(1))(6(5))" ;
Node root = treeFromString(str, 0 , str.length() - 1 );
preOrder(root);
}
}
Python
class newNode:
def __init__( self , data):
self .data = data
self .left = self .right = None
def preOrder(node):
if (node = = None ):
return
print (node.data, end = ' ' )
preOrder(node.left)
preOrder(node.right)
def findIndex( Str , si, ei):
if (si > ei):
return - 1
s = []
for i in range (si, ei + 1 ):
if ( Str [i] = = '(' ):
s.append( Str [i])
elif ( Str [i] = = ')' ):
if (s[ - 1 ] = = '(' ):
s.pop( - 1 )
if len (s) = = 0 :
return i
return - 1
def treeFromString( Str , si, ei):
if (si > ei):
return None
root = newNode( ord ( Str [si]) - ord ( '0' ))
index = - 1
if (si + 1 < = ei and Str [si + 1 ] = = '(' ):
index = findIndex( Str , si + 1 , ei)
if (index ! = - 1 ):
root.left = treeFromString( Str , si + 2 ,
index - 1 )
root.right = treeFromString( Str , index + 2 ,
ei - 1 )
return root
if __name__ = = '__main__' :
Str = "4(2(3)(1))(6(5))"
root = treeFromString( Str , 0 , len ( Str ) - 1 )
preOrder(root)
C#
using System;
using System.Collections.Generic;
public class GFG
{
public
class Node
{
public
int data;
public
Node left, right;
};
static Node newNode( int data)
{
Node node = new Node();
node.data = data;
node.left = node.right = null ;
return (node);
}
static void preOrder(Node node)
{
if (node == null )
return ;
Console.Write( "{0} " , node.data);
preOrder(node.left);
preOrder(node.right);
}
static int findIndex(String str, int si, int ei)
{
if (si > ei)
return -1;
Stack< char > s = new Stack< char >();
for ( int i = si; i <= ei; i++)
{
if (str[i] == '(' )
s.Push(str[i]);
else if (str[i] == ')' )
{
if (s.Peek() == '(' )
{
s.Pop();
if (s.Count==0)
return i;
}
}
}
return -1;
}
static Node treeFromString(String str, int si, int ei)
{
if (si > ei)
return null ;
int num = 0;
while (si <= ei && str[si] >= '0' && str[si] <= '9' )
{
num *= 10;
num += (str[si] - '0' );
si++;
}
si--;
Node root = newNode(num);
int index = -1;
if (si + 1 <= ei && str[si+1] == '(' )
index = findIndex(str, si + 1, ei);
if (index != -1)
{
root.left = treeFromString(str, si + 2, index - 1);
root.right
= treeFromString(str, index + 2, ei - 1);
}
return root;
}
public static void Main(String[] args)
{
String str = "4(2(3)(1))(6(5))" ;
Node root = treeFromString(str, 0, str.Length - 1);
preOrder(root);
}
}
Javascript
class Node
{
constructor()
{
this .data = 0;
this .left = this .right = null ;
}
}
function newNode(data)
{
let node = new Node();
node.data = data;
node.left = node.right = null ;
return (node);
}
function preOrder(node)
{
if (node == null )
return ;
console.log(node.data + " " );
preOrder(node.left);
preOrder(node.right);
}
function findIndex(str, si, ei)
{
if (si > ei)
return -1;
let s = [];
for (let i = si; i <= ei; i++)
{
if (str[i] == '(' )
s.push(str[i]);
else if (str[i] == ')' )
{
if (s[s.length-1] == '(' )
{
s.pop();
if (s.length == 0)
return i;
}
}
}
return -1;
}
function treeFromString(str,si,ei)
{
if (si > ei)
return null ;
let num = 0;
while (si <= ei && str[si] >= '0' && str[si] <= '9' )
{
num *= 10;
num += (str[si] - '0' );
si++;
}
si--;
let root = newNode(num);
let index = -1;
if (si + 1 <= ei && str[si + 1] == '(' )
index = findIndex(str, si + 1, ei);
if (index != -1)
{
root.left = treeFromString(str, si + 2, index - 1);
root.right
= treeFromString(str, index + 2, ei - 1);
}
return root;
}
let str = "14(2(3)(1))(6(5))" ;
let root = treeFromString(str, 0, str.length - 1);
preOrder(root);
Time Complexity: O(N2)
Auxiliary Space: O(N)
Another recursive approach:
Algorithm:
- The very first element of the string is the root.
- If the next two consecutive elements are "(" and ")", this means there is no left child otherwise we will create and add the left child to the parent node recursively.
- Once the left child is added recursively, we will look for consecutive "(" and add the right child to the parent node.
- Encountering ")" means the end of either left or right node and we will increment the start index
- The recursion ends when the start index is greater than equal to the end index
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node* left;
struct Node* right;
Node( int val)
{
data = val;
left = right = NULL;
}
};
Node* constructtree(string s, int * start)
{
if (s.size() == 0 || *start >= s.size())
return NULL;
int num = 0;
while (*start < s.size() && s[*start] != '('
&& s[*start] != ')' ) {
int num_here = ( int )(s[*start] - '0' );
num = num * 10 + num_here;
*start = *start + 1;
}
struct Node* root = NULL;
if (num > 0)
root = new Node(num);
if (*start < s.size() && s[*start] == '(' ) {
*start = *start + 1;
root->left = constructtree(s, start);
}
if (*start < s.size() && s[*start] == ')' )
{
*start = *start + 1;
return root;
}
if (*start < s.size() && s[*start] == '(' ) {
*start = *start + 1;
root->right = constructtree(s, start);
}
if (*start < s.size() && s[*start] == ')' )
*start = *start + 1;
return root;
}
void preorder(Node* root)
{
if (root == NULL)
return ;
cout << root->data << " " ;
preorder(root->left);
preorder(root->right);
}
int main()
{
string s = "4(2(3)(1))(6(5))" ;
int start = 0;
Node* root = constructtree(s, &start);
preorder(root);
return 0;
}
Java
import java.io.*;
import java.util.*;
class GFG{
static class Node
{
int data;
Node left,right;
Node( int data)
{
this .data = data;
this .left = this .right = null ;
}
}
static int start = 0 ;
static Node constructTree(String s)
{
if (s.length() == 0 || s == null )
{
return null ;
}
if (start >= s.length())
return null ;
boolean neg = false ;
if (s.charAt(start) == '-' )
{
neg = true ;
start++;
}
int num = 0 ;
while (start < s.length() &&
Character.isDigit(s.charAt(start)))
{
int digit = Character.getNumericValue(
s.charAt(start));
num = num * 10 + digit;
start++;
}
if (neg)
num = -num;
Node node = new Node(num);
if (start >= s.length())
{
return node;
}
if (start < s.length() && s.charAt(start) == '(' )
{
start++;
node.left = constructTree(s);
}
if (start < s.length() && s.charAt(start) == ')' )
{
start++;
return node;
}
if (start < s.length() && s.charAt(start) == '(' )
{
start++;
node.right = constructTree(s);
}
if (start < s.length() && s.charAt(start) == ')' )
{
start++;
return node;
}
return node;
}
public static void printTree(Node node)
{
if (node == null )
return ;
System.out.println(node.data + " " );
printTree(node.left);
printTree(node.right);
}
public static void main(String[] args)
{
String s = "4(2(3)(1))(6(5))" ;
Node root = constructTree(s);
printTree(root);
}
}
Python3
class newNode:
def __init__( self , data):
self .data = data
self .left = self .right = None
def preOrder(node):
if (node = = None ):
return
print (node.data, end = " " )
preOrder(node.left)
preOrder(node.right)
def treeFromStringHelper(si, ei, arr, root):
if si[ 0 ] > = ei:
return None
if arr[si[ 0 ]] = = "(" :
if arr[si[ 0 ] + 1 ] ! = ")" :
if root.left is None :
if si[ 0 ] > = ei:
return
new_root = newNode(arr[si[ 0 ] + 1 ])
root.left = new_root
si[ 0 ] + = 2
treeFromStringHelper(si, ei, arr, new_root)
else :
si[ 0 ] + = 2
if root.right is None :
if si[ 0 ] > = ei:
return
if arr[si[ 0 ]] ! = "(" :
si[ 0 ] + = 1
return
new_root = newNode(arr[si[ 0 ] + 1 ])
root.right = new_root
si[ 0 ] + = 2
treeFromStringHelper(si, ei, arr, new_root)
else :
return
if arr[si[ 0 ]] = = ")" :
if si[ 0 ] > = ei:
return
si[ 0 ] + = 1
return
return
def treeFromString(string):
root = newNode(string[ 0 ])
if len (string) > 1 :
si = [ 1 ]
ei = len (string) - 1
treeFromStringHelper(si, ei, string, root)
return root
if __name__ = = '__main__' :
Str = "4(2(3)(1))(6(5))"
root = treeFromString( Str )
preOrder(root)
C#
using System;
class GFG {
class Node {
public int data;
public Node left, right;
public Node( int data)
{
this .data = data;
left = right = null ;
}
}
static int start = 0;
static Node constructTree( string s)
{
if (s.Length == 0 || s == null )
{
return null ;
}
if (start >= s.Length)
return null ;
bool neg = false ;
if (s[start] == '-' )
{
neg = true ;
start++;
}
int num = 0;
while (start < s.Length &&
Char.IsDigit(s[start]))
{
int digit = ( int )Char.GetNumericValue(
s[start]);
num = num * 10 + digit;
start++;
}
if (neg)
num = -num;
Node node = new Node(num);
if (start >= s.Length)
{
return node;
}
if (start < s.Length && s[start] == '(' )
{
start++;
node.left = constructTree(s);
}
if (start < s.Length && s[start] == ')' )
{
start++;
return node;
}
if (start < s.Length && s[start] == '(' )
{
start++;
node.right = constructTree(s);
}
if (start < s.Length && s[start] == ')' )
{
start++;
return node;
}
return node;
}
static void printTree(Node node)
{
if (node == null )
return ;
Console.Write(node.data + " " );
printTree(node.left);
printTree(node.right);
}
static void Main()
{
string s = "4(2(3)(1))(6(5))" ;
Node root = constructTree(s);
printTree(root);
}
}
Javascript
<script>
class Node
{
constructor(data)
{
this .data=data;
this .left = this .right = null ;
}
}
let start = 0;
function constructTree(s)
{
if (s.length == 0 || s == null )
{
return null ;
}
if (start >= s.length)
return null ;
let neg = false ;
if (s[start] == '-' )
{
neg = true ;
start++;
}
let num = 0;
while (start < s.length && !isNaN(s[start] -
parseInt(s[start])))
{
let digit = parseInt(
s[start]);
num = num * 10 + digit;
start++;
}
if (neg)
num = -num;
let node = new Node(num);
if (start >= s.length)
{
return node;
}
if (start < s.length && s[start] == '(' )
{
start++;
node.left = constructTree(s);
}
if (start < s.length && s[start] == ')' )
{
start++;
return node;
}
if (start < s.length && s[start] == '(' )
{
start++;
node.right = constructTree(s);
}
if (start < s.length && s[start] == ')' )
{
start++;
return node;
}
return node;
}
function printTree(node)
{
if (node == null )
return ;
document.write(node.data + " " );
printTree(node.left);
printTree(node.right);
}
let s = "4(2(3)(1))(6(5))" ;
let root = constructTree(s);
printTree(root);
</script>
This article is contributed by Chhavi. If you like GeeksforGeeks and would like to contribute, you can also write an article using contribute.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Source: https://www.geeksforgeeks.org/construct-binary-tree-string-bracket-representation/
0 Response to "program to draw binary search tree of a string"
Post a Comment